Full Binary Tree
A full binary tree, also known as a proper or strictly binary tree, is a binary tree in which every node has either 0 or 2 children. This tutorial directly addresses what a full binary tree is, demonstrates examples using array notation and graphical diagrams, explains in detail why certain trees are or are not full binary trees, and discusses their applications.
Definition of Full Binary Tree
A full binary tree is defined as a binary tree in which every node is either a leaf (has no children) or an internal node with exactly two children. No node in a full binary tree has only one child.
Example 1: Full Binary Tree
In this example, we represent a full binary tree using an array.
Example Array: [1, 2, 3, 4, 5, 6, 7]
The array notation follows the convention that for a node at index i, its left child is at index 2*i + 1 and its right child is at index 2*i + 2.
Graphical Diagram Representation:
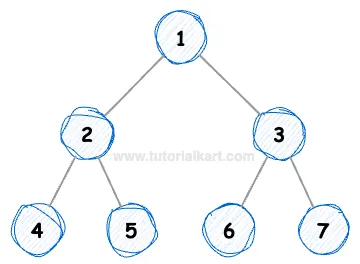
Explanation:
- The root of the tree is at index 0, which is
1. - The left child of
1is at index 1 (2) and the right child is at index 2 (3). - For node
2at index 1, its children are at indices 3 (4) and 4 (5). - For node
3at index 2, its children are at indices 5 (6) and 6 (7). - Every internal node (1, 2, and 3) has exactly two children, and all leaf nodes (4, 5, 6, and 7) have no children.
- Thus, the tree represented by the array is a full binary tree.
Example 2: Non-Full Binary Tree and Comparison
In this example, we illustrate a tree that is not full by using an array representation where one internal node is missing a child. We use - to denote a missing node.
Example Array: [1, 2, 3, 4, -, 6, 7]
Graphical Diagram Representation:
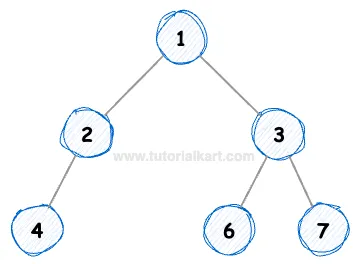
(Note: Node 2 is missing its right child.)
Explanation:
- The root node is
1at index 0, with children2(index 1) and3(index 2). - For node
2at index 1, the left child is4at index 3, but the right child is missing, as indicated by-at index 4. - Since node
2does not have exactly two children, the tree does not meet the criteria for a full binary tree. - Even though node
3at index 2 appears to have two children (6and7), the missing child for node2is enough to classify the overall tree as not full.
Example 3: Full Binary Tree with a Leaf Subtree
In this example, we illustrate a full binary tree where one subtree is a leaf node (i.e., it has no children) while the other subtree is a complete binary subtree. This shows that even if some subtrees do not have further children, the overall tree can still be considered a full binary tree as long as every internal node has exactly two children.
Example Array: [10, 20, 30, -, -, 40, 50]
Graphical Diagram Representation:
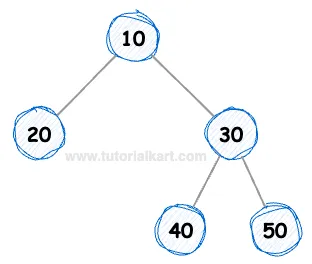
Explanation:
10is the root node with two children:20and30.20is a leaf node with no children. In a full binary tree, it is acceptable for a node to have no children.30is an internal node and has exactly two children:40and50.- Both
40and50are leaf nodes (they do not have any children). - Since every internal node (
10and30) has exactly two children, and all other nodes are leaves, the tree qualifies as a full binary tree.
Applications of Full Binary Trees
Full binary trees are useful in various areas of computer science due to their balanced and predictable structure. Some common applications include:
- Expression Trees: Used in compilers and calculators where internal nodes represent operators and leaf nodes represent operands. The full structure ensures clear operator precedence.
- Decision Trees: Utilized in machine learning and decision-making processes, where each decision node splits into exactly two branches.
- Data Structures: Serve as the basis for heaps and other tree-based data structures, ensuring efficient access and manipulation.
- Network Routing and Data Compression: Certain algorithms leverage full binary trees for balanced and efficient processing.
Summary
In this tutorial, we defined a full binary tree as a binary tree in which every node has either 0 or 2 children. We provided detailed examples using array notation and graphical diagrams to illustrate what makes a tree full or not full. Additionally, we discussed several practical applications of full binary trees in computer science. Understanding these concepts is fundamental for exploring more advanced topics in tree data structures and algorithms.
