Introduction to 30-60-90 Triangle Formula
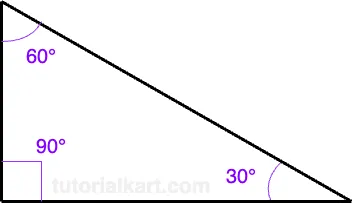
A 30-60-90 triangle is a special type of right triangle that has angle measures of 30°, 60°, and 90°.
What makes this triangle unique is that the sides of the triangle follow a consistent ratio, allowing us to easily calculate the lengths of any side if we know one of them.
In this tutorial, we’ll cover the characteristics of a 30-60-90 triangle, the formula to calculate the sides, and how to apply it in various examples.
Properties of a 30-60-90 Triangle
In a 30-60-90 triangle:
- The 90° angle is the right angle.
- The 30° angle is the smallest angle.
- The 60° angle is the second largest angle.
- The sides of the triangle follow a specific ratio based on these angles.
Side Length Ratios
The sides of a 30-60-90 triangle are always in the ratio:
\[ 1 : \sqrt{3} : 2 \]
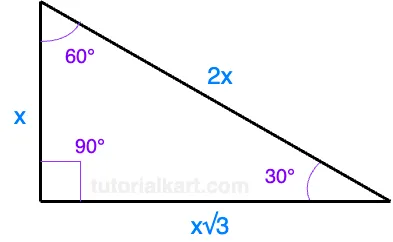
Here’s how the ratio corresponds to the sides of the triangle:
- The shortest side (opposite the 30° angle) is \( x \), which is height in the above diagram.
- The longer leg (opposite the 60° angle) is \( x \sqrt{3} \), which is base in the above diagram.
- The hypotenuse (opposite the 90° angle) is \( 2x \).
Knowing this ratio, you can determine the length of any side of the triangle as long as you know one of the sides.
Formula for the 30-60-90 Triangle
If you know one side of a 30-60-90 triangle, you can use the following formulas to find the other sides:
If you know the shorter leg (opposite the 30° angle):
\[ \text{Longer leg} = x \sqrt{3} \]
\[ \text{Hypotenuse} = 2x \]
If you know the longer leg (opposite the 60° angle):
\[ \text{Shorter leg} = \frac{\text{Longer leg}}{\sqrt{3}} \]
\[ \text{Hypotenuse} = 2 \times \left(\frac{\text{Longer leg}}{\sqrt{3}}\right) \]
If you know the hypotenuse:
\[ \text{Shorter leg} = \frac{\text{Hypotenuse}}{2} \]
\[ \text{Longer leg} = \frac{\text{Hypotenuse}}{2} \times \sqrt{3} \]
Example Calculations
Let’s look at some example calculations to understand how these formulas work.
Example 1: Finding the longer leg and hypotenuse
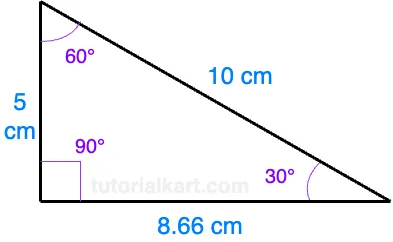
Given a 30-60-90 triangle where the shorter leg (opposite the 30° angle) is 5 cm, we can calculate the lengths of the other sides:
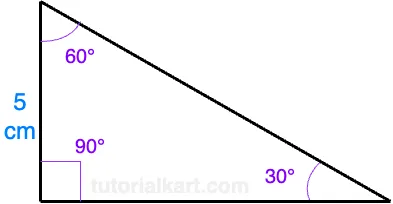
Using the formula for the longer leg:
\[ \text{Longer leg} = 5 \times \sqrt{3} \approx 5 \times 1.732 = 8.66 \, \text{cm} \]
Using the formula for the hypotenuse:
\[ \text{Hypotenuse} = 2 \times 5 = 10 \, \text{cm} \]
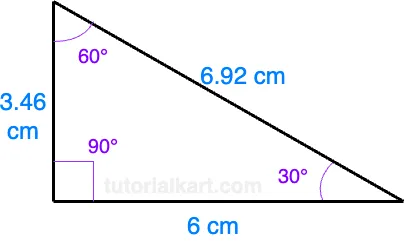
Example 2: Finding the shorter leg and hypotenuse
If the longer leg (opposite the 60° angle) is 6 cm, we can find the shorter leg and the hypotenuse:
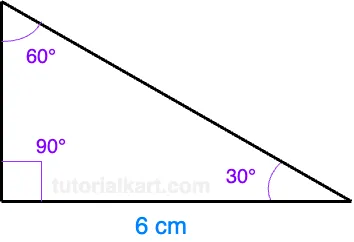
Using the formula for the shorter leg:
\[ \text{Shorter leg} = \frac{6}{\sqrt{3}} \approx \frac{6}{1.732} = 3.46 \, \text{cm} \]
Using the formula for the hypotenuse:
\[ \text{Hypotenuse} = 2 \times 3.46 = 6.92 \, \text{cm} \]