Rhombus
Welcome to tutorial on Rhombus.
Rhombus is a quadrilateral (geometrical shape with four sides) in which all the sides are equal.
Following diagram represents a rhombus.

Let us name the vertices, mark the angles and discuss about properties of rhombus in detail.
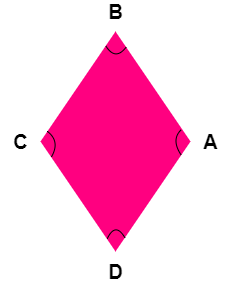
Following table gives a overview on the properties of a Rhombus.
| Property | Values | Information |
| Vertices | A, B, C, D | |
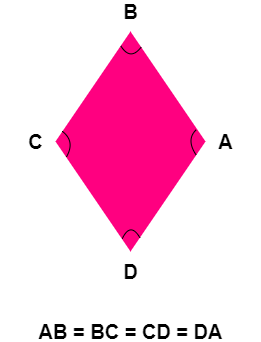
| Sides | AB, BC. CD, DA | AB = BC = CD = DA |
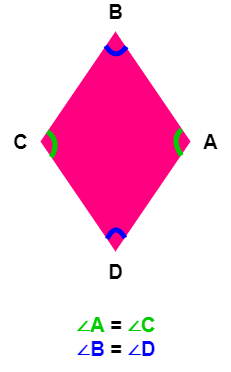
| Angles | ∠A, ∠B, ∠C, ∠D | ∠A = ∠C, ∠C = ∠D, ∠A+∠B=180, ∠C+∠D=180 |
| Diagonals | AC, BD | AC ⟂ BD |
Properties of Rhombus
Property 1: All sides of a Rhombus are equal in length
This is of course from the definition of a rhombus, all sides of a Rhombus are equal in length.
Property 2: Opposite angles are equal
When it comes to angles of a Rhombus, opposite pairs of angles are equal. This is a side effect from the fact that all the sides of a Rhombus are equal.
Property 3: Sum of any two adjacent angles is 180 degrees
Based on the fact that opposite sides are parallel, sum of any two adjacent angles in a Rhombus is 180 degrees.
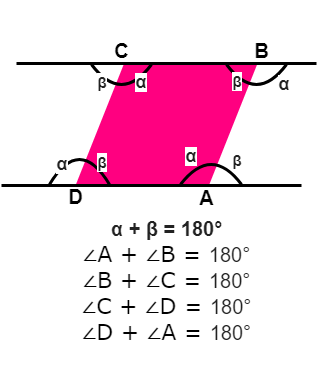
In the above diagram, the sides DA and BC are extended to understand the angles.
Property 4: Opposite sides are parallel to each other
In a Rhombus, opposite sides are parallel to each other. Of-course in any quadrilateral, where all the sides are equal, opposite sides are parallel to each other.
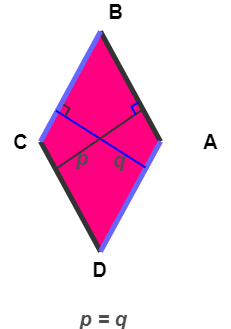
Property 5: Shortest Distance between the parallel sides, of the two sets, are equal
If p is the distance between the parallel sides AB and CD, and q is the distance between the parallel sides BC and DA; then these two distances are equal p = q .
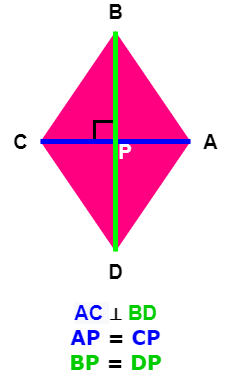
Property 6: Diagonals are perpendicular and bisect each other
In any quadrilateral, where all sides are equal, the diagonals are perpendicular to each other and bisect each other into equal halves.
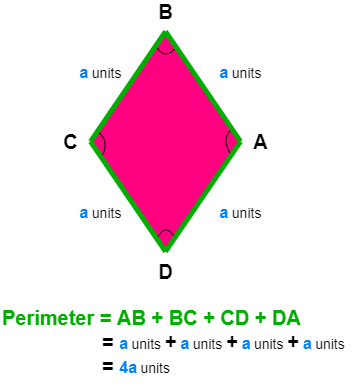
Perimeter of Rhombus
Perimeter is the distance traveled when you cover all the sides of the Rhombus.
Area of Rhombus
There are two ways through which you can find the Area of Rhombus. These ways are categorized based on the set of parameters that can be used to define a Rhombus.
Way 1: Using Length of a Side and an Angle
Set of a length and an angle can define a Rhombus. In this method, we will use length of a side and an angle at any vertex, to find the area of the Rhombus.
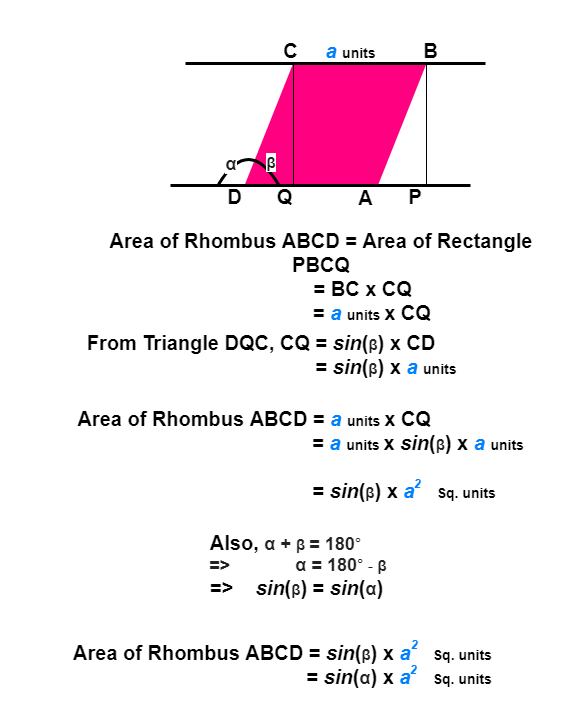
Way 2: Using the lengths of Diagonals
You can also define a Rhombus using only the diagonals. Hence, in this method, we will use the length of diagonals as parameters in finding the area of Rhombus.
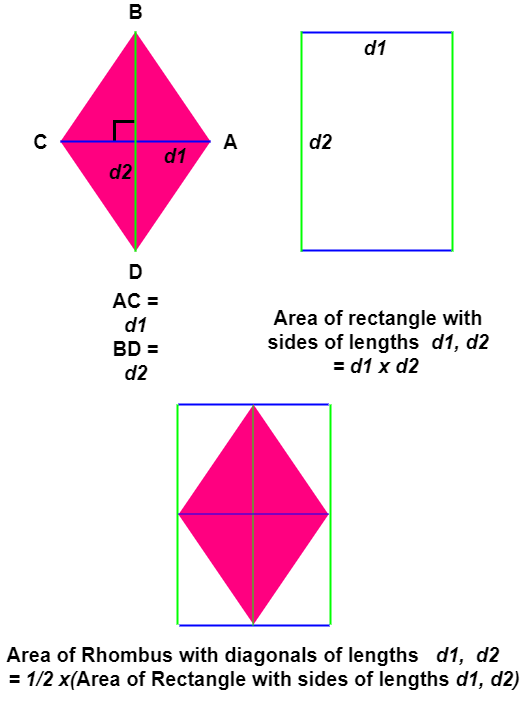
Therefore, Area of Rhombus with diagonals of lengths d1, d2 = (d1 x d2)/2.
Conclusion
In this Geometry Tutorial, we learned about Rhombus, properties of Rhombus, how to find Perimeter of Rhombus and Area of Rhombus.
